IntervalRootFinding.jl
This package provides guaranteed methods for finding roots of functions $f: \mathbb{R}^n \to \mathbb{R}^n$ with $n \ge 1$, i.e. vectors (or scalars, for $n=1$) $\mathbb{x}$ for which $f(\mathbb{x}) = \mathbb{0}$. In principle, it guarantees to find all roots inside a given box in $\mathbb{R}^n$, or report subboxes for which it is unable to provide guarantees.
To do so, it uses methods from interval analysis, using interval arithmetic from the IntervalArithmetic.jl package by the same authors.
While this package aimed at providing guaranteed results and despite our best efforts and test suite, some bugs may remain and there are several known issues with corner cases. Please look at the issue tracker and report there any odd and/or incorrect behavior.
Basic 1D example
To begin, we need a standard Julia function and an interval in which to search roots of that function. Intervals use the Interval type provided by the IntervalArithmetic.jl package Intervals are generally constructed using the .. syntax (from the IntervalArithmetic.Symbols submodule), a..b representing the closed interval $[a, b]$.
When provided with this information, the roots function will return a vector of all roots of the function in the given interval.
Example:
julia> using IntervalArithmetic, IntervalArithmetic.Symbols, IntervalRootFinding
julia> rts = roots(x -> x^2 - 2x, 0..10)
2-element Vector{Root{Interval{Float64}}}:
Root([0.0, 3.73849e-08]_com_NG, :unknown)
Root([1.999999, 2.00001]_com_NG, :unique)The roots are returned as Root objects, containing an interval and the status of that interval, represented as a Symbol. There are two possible types of root status, as shown in the example:
:unique: the given interval contains exactly one root of the function,:unknown: the given interval may or may not contain one or more roots; the algorithm used was unable to come to a conclusion.
The second status is still informative, since all regions of the original search interval not contained in any of the returned root intervals is guaranteed not to contain any root of the function. In the above example, we know that the function has no root in the interval $[2.1, 10]$, for example.
There are several known situations where the uniqueness (and existence) of a solution cannot be determined by the interval algorithms used in the package:
- If the solution is on the boundary of the interval (as in the previous example);
- If the derivative of the solution is zero at the solution.
In particular, the second condition means that multiple roots cannot be proven to be unique. For example:
julia> g(x) = (x^2 - 2)^2 * (x^2 - 3)
g (generic function with 1 method)
julia> roots(g, -10..10)
4-element Vector{Root{Interval{Float64}}}:
Root([-1.73206, -1.73205]_com_NG, :unique)
Root([-1.41422, -1.41421]_com, :unknown)
Root([1.41421, 1.41422]_com, :unknown)
Root([1.73205, 1.73206]_com_NG, :unique) Here we see that the two double roots are reported as being possible roots without guarantee and the simple roots have been proved to be unique.
Basic multi-dimensional example
For dimensions $n > 1$, the function passed to roots must take an array as argument and return an array. The initial search region is an array of interval.
Here we give a 3D example:
julia> function g( (x1, x2, x3) )
return [
x1^2 + x2^2 + x3^2 - 1,
x1^2 + x3^2 - 0.25,
x1^2 + x2^2 - 4x3
]
end
g (generic function with 1 method)
julia> X = -5..5
[-5.0, 5.0]_com
julia> rts = roots(g, [X, X, X])
4-element Vector{Root{Vector{Interval{Float64}}}}:
Root(Interval{Float64}[[-0.440763, -0.440762]_com_NG, [-0.866026, -0.866025]_com_NG, [0.236067, 0.236069]_com_NG], :unique)
Root(Interval{Float64}[[-0.440763, -0.440762]_com_NG, [0.866025, 0.866026]_com_NG, [0.236067, 0.236069]_com_NG], :unique)
Root(Interval{Float64}[[0.440762, 0.440763]_com_NG, [-0.866026, -0.866025]_com_NG, [0.236067, 0.236069]_com_NG], :unique)
Root(Interval{Float64}[[0.440762, 0.440763]_com_NG, [0.866025, 0.866026]_com_NG, [0.236067, 0.236069]_com_NG], :unique)Thus, the system admits four unique roots in the box $[-5, 5]^3$.
Moreover, the package is compatible with StaticArrays.jl. Usage of static arrays is recommended to increase performance.
julia> using StaticArrays
julia> h((x, y)) = SVector(x^2 - 4, y^2 - 16)
h (generic function with 1 method)
julia> roots(h, SVector(X, X))
4-element Vector{Root{SVector{2, Interval{Float64}}}}:
Root(Interval{Float64}[[-2.00001, -1.999999]_com_NG, [-4.00001, -3.999999]_com_NG], :unique)
Root(Interval{Float64}[[-2.00001, -1.999999]_com_NG, [3.999999, 4.00001]_com_NG], :unique)
Root(Interval{Float64}[[1.999999, 2.00001]_com_NG, [-4.00001, -3.999999]_com_NG], :unique)
Root(Interval{Float64}[[1.999999, 2.00001]_com_NG, [3.999999, 4.00001]_com_NG], :unique)Vector types
The multidimensional search region (formerly represented as IntervalBox) can be represented by both Vector and SVector (from StaticArrays.jl) of Interval, the latter giving better performances.
However, the types used must be consistent: when using roots(f, X), f(X) should have the same type as X. In particular, if f return a SVector of Interval, make sure to use a SVector of Interval for the initial search region X.
Moreover, if X and f(X) are SVector, and the jacobian function is given explicitly, then the jacobian function should return a SMatrix of the appropriate size.
Mixing between (standard) Vector and (static) SVector may result in errors or bad performances.
Note that the function doesn't need to be defined specifically for Interval inputs: for example f(X) = [X[1]^2 - 2, X[2]^2 - 3] returns either a Vector{Float64} or a Vector{Interval} depending on the input.
Furthermore, when you know that the number given as literals are parsed exactly (which is typically not guaranteed for floating points inputs), you can avoid the NG flag that arise from mixing numbers and intervals, with the @exact macro:
julia> f(X) = @exact [X[1]^2 - 2, X[2]^2 - 3]
f (generic function with 1 method)
julia> x = [interval(0, 5), interval(0, 5)]
2-element Vector{Interval{Float64}}:
[0.0, 5.0]_com
[0.0, 5.0]_com
julia> roots(f, x)
1-element Vector{Root{Vector{Interval{Float64}}}}:
Root(Interval{Float64}[[1.41421, 1.41422]_com, [1.73205, 1.73206]_com], :unique)This macro does not disturb the function when called with non-interval inputs:
julia> f([1.2, 2.2])
2-element Vector{Float64}:
-0.56
1.8400000000000007Stationary points
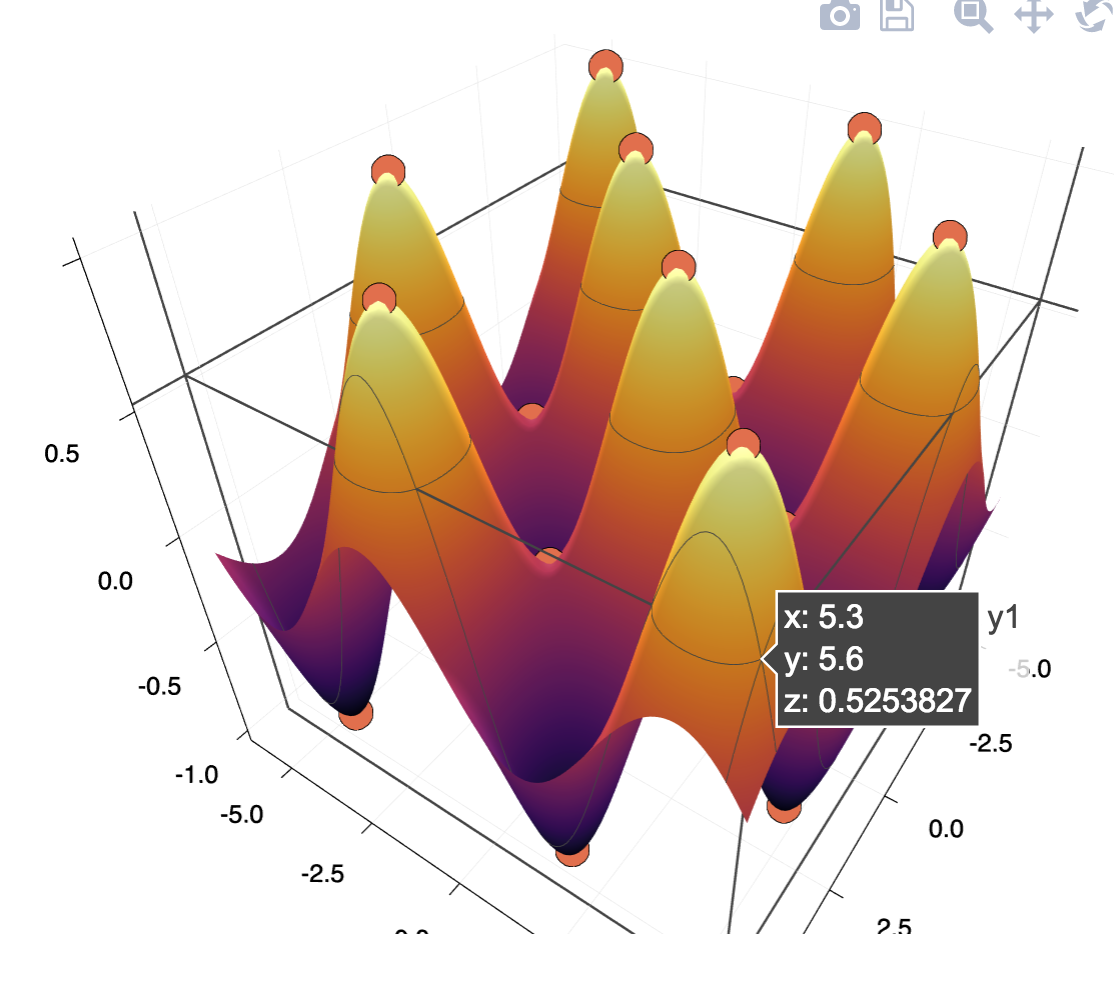
Stationary points of a function $f:\mathbb{R}^n \to \mathbb{R}$ may be found as zeros of the gradient of $f$. The gradient can be computed using ForwardDiff.jl:
julia> using ForwardDiff: gradient
julia> f( (x, y) ) = sin(x) * sin(y)
f (generic function with 1 method)
julia> ∇f(x) = gradient(f, x) # gradient operator from the package
(::#53) (generic function with 1 method)
julia> rts = roots(∇f, SVector(interval(-5, 6), interval(-5, 6)) ; abstol = 1e-5)
25-element Vector{Root{SVector{2, Interval{Float64}}}}:
Root(Interval{Float64}[[-4.7124, -4.71238]_com, [-4.7124, -4.71238]_com], :unique)
Root(Interval{Float64}[[-3.1416, -3.14159]_com, [-3.1416, -3.14159]_com], :unique)
⋮
[output skipped for brevity]Now let's find the midpoints and plot them:
midpoints = [mid.(root_region(rt)) for rt in rts]
xs = first.(midpoints)
ys = last.(midpoints)
using Plots; plotlyjs()
surface(-5:0.1:6, -6:0.1:6, (x,y) -> f([x, y]))
scatter!(xs, ys, f.(midpoints))