Overview

This package contains routines to perform numerical linear algebra using interval arithmetic. This can be used both for rigorous computations and uncertainty propagation.

An first overview of the package was given at JuliaCon 2021, the slides are available here.

Features

• enclosure of the solution of interval linear systems
• exact characterization of the solution set of interval linear systems using Oettli-Präger
• verified solution of floating point linear systems
• enclosure of eigenvalues of interval matrices
• verified computation of eigenvalues and eigenvectors of floating point matrices

Installation

Open a Julia session and enter

using Pkg; Pkg.add("IntervalLinearAlgebra")

this will download the package and all the necessary dependencies for you. Next you can import the package with

using IntervalLinearAlgebra

and you are ready to go.

Quickstart

using IntervalLinearAlgebra, LazySets, Plots

A = [2..4 -1..1; -1..1 2..4]
b = [-2..2, -1..1]

Xenclose = solve(A, b)
polytopes = solve(A, b, LinearOettliPrager())

plot(UnionSetArray(polytopes), ratio=1, label="solution set", legend=:top)
plot!(IntervalBox(Xenclose), label="enclosure")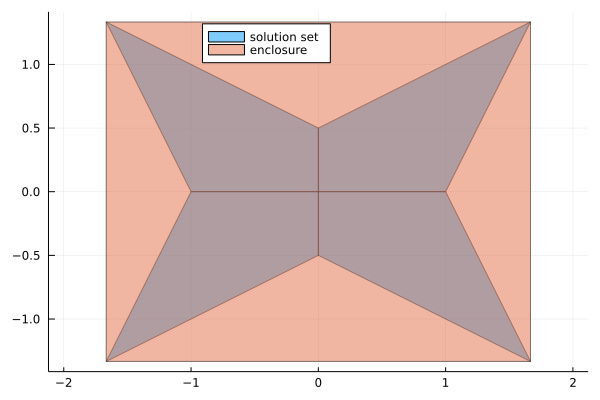

Citation

If you use this package in your work, please cite it as

@software{ferranti2021interval,
author = {
            Luca Feranti and
            Marcelo Forets and
            David P. Sanders
         },
title  = {IntervalLinearAlgebra.jl: linear algebra done rigorously},
month  = {9},
year   = {2021},
doi    = {10.5281/zenodo.5363563},
url    = {https://github.com/juliaintervals/IntervalLinearAlgebra.jl}
}